搜题请搜索小程序“爱下问搜题”
问题 问答题

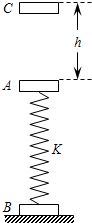
如图所示，质量m1=2kg的物体A与一劲度系数为k=500N/m的轻弹簧相连，弹簧的另一端与地面上的质量为m2=1kg的物体B相连，弹簧竖起．A、B均处于静止状态．另有一质量为m3=1kg的物体C从物体A的正上方距离h=0.45m处自由下落．落到A上立刻与A粘连并一起向下运动，其速度为1m/s，它们到达最低点后又向上运动，最终恰好能使B离开地面但不继续上升．（A、B、C均可视为质点，g取10m/s2）

（1）求C与A碰撞前的速度V；

（2）从AC一起运动直至最高点的过程中弹簧对AC整体做的功．

答案

（1）设物体C与A碰撞前速度为V0，则根据动能定理：m3gh=

m3
V20
2
-0

解得：V0=3m/s．

（2）根据F=kx，开始时弹簧压缩量x1=

m1g
k
=0.04m

B刚要离开地面时弹簧伸长量x2=

m2g
k
=0.02m

则AC一起运动的最高点和碰撞位置的距离为h′=x1+x2=0.06m

设从AC一起运动直至最高点的过程中弹簧弹力做功为W，根据动能定理：W-(m1+m3)gh′=0-

(m1+m3)V2
2

解得W=0.3J．

填空题

有人设计了一套实验室分馏芳香油的五个步骤：

①将蒸馏烧瓶固定在铁架台上，在蒸馏烧瓶上塞好带温度计的橡胶塞。

②连接好冷凝管，把冷凝管固定在铁架台上，将冷凝管进水口的橡皮管的另一端与水龙头相连，将和出水口相接的橡皮管的另一端放在水槽中。

③把酒精灯放在铁架台上，根据酒精灯的高度确定铁圈的高度，放好石棉网。

④向蒸馏烧瓶中放入几片碎瓷片，再用漏斗向烧瓶中加入原料，塞好带温度计的橡胶塞，把接收器连接在冷凝管的末端，并伸入接收装置(如锥形瓶)中。

⑤检查气密性。

(1)玫瑰精油高温______分解，______溶于水，_____溶于有机溶剂，可以采用______提取，再经_____过程即可得到较纯净的玫瑰精油。

(2)上述实验正确的操作顺序是：_______→_______→_______→______→________。

(3)冷凝管里水流的方向与蒸汽的流向____________。

(4)温度计水银球应放在__________位置，以测量___________的温度。

(5)在蒸馏烧瓶中加入几片碎瓷片，目的是_________。

(6)通过蒸馏，得到的是_________，若想得到纯净的玫瑰精油，需____________，首先____________，目的是_________，静置的__________(填“上口”或“下口”)得到产物。

(7)提取玫瑰精油的原理是________________。
查看答案
问答题

已知将氯气通入浓氨水中可以发生如下反应：3Cl2+8NH3=6NH4Cl+N2

（1）用双线桥标出电子转移的方向和数目______

（2）当有17g的NH3被氧化时，生成的NH4Cl的质量是______．
查看答案