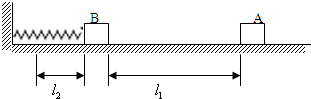
一根弹性细绳（遵循胡克定律）原长为l，劲度系数为k，将其一端穿

问题问答题

一根弹性细绳（遵循胡克定律）原长为l，劲度系数为k，将其一端穿过一个光滑小孔O（其在水平地面上的投影点为O’），系在一个质量为m的滑块A上，A放在水平地面上．小孔O离绳固定端的竖直距离为l，离水平地面高度为h（h＜mg/k），滑块A与水平地面间的最大静摩擦力为正压力的μ倍．问：

（1）当滑块与O’点距离为r时，弹性细绳对滑块A的拉力为多大？

（2）滑块处于怎样的区域内时可以保持静止状态？

答案

（1）从几何关系看出：弹性细绳的伸长量为△x=

h2+r2

弹性细绳对滑块A的拉力为F_T=k△x=k

h2+r2

（2）设A静止时离O′的距离为r，此位置处A将受到四个力的作用如图：

对F_T正交分解，由于处于平衡状态所以有：

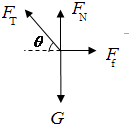竖直方向：F_N+F_Tsinθ=mg，

水平方向：F_Tcosθ=F_f

而F_T=k

sinθ

，F_fmax=μF_{N
所以有：k
h
sinθ
cosθ=f≤f_max=μ（mg-kh）
其中
h
sinθ
cosθ=r
即r≤
μ(mg-kh)
k
这表明，滑块可以静止在以O′为圆心，
μ(mg-kh)
k
为半径的圆域内的任意位置．
答：（1）当滑块与O’点距离为r时，弹性细绳对滑块A的拉力为k
h2+r2
；
（2）滑块可以静止在以O’为圆心，
μ(mg-kh)
k
为半径的圆域内的任意位置．}