问题
问答题
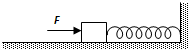
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体接触(未连接),弹簧水平且无形变,用水平力F缓慢推动物体,在弹性限度内弹簧长度被压缩了x0,此时物体静止,撤去F后,物体开始向左运动,运动的最大距离为4x0,物体与水平面间的动摩擦因数为μ,重力加速度为g,问:
①撤去F后,物体刚运动时的加速度多大?
②物体做匀减速运动的时间是多长?
③物体从开始向左运动到速度达到最大值,发生的位移多大?
答案
(1)物体刚运动时,水平方向合力为:
F=kx0-μmg
由牛顿第二定律得:
a=
=F m
-μgkx0 m
(2)物体匀减速的加速度大小为:
a=μg
从弹簧恢复原长开始,物块做匀减速运动,故匀减速运动的位移为:
x=3x0
由运动学公式得:
x=
at21 2
联立解得:t=6x0 μg
(3)当弹力大小等于滑动摩擦力时,物块速度最大,选静止时的位置为参考位置,物体发生位移为x1,由胡克定律得:kx1=μmg
所以:x1=μmg k
答:(1)撤去F后,物体刚运动时的加速度为
-μgkx0 m
(2)物体做匀减速运动的时间是6x0 μg
(3)物体从开始向左运动到速度达到最大值,发生的位移μmg k
