问题
多选题
如图甲所示,劲度系数为k的轻弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处由静止释放,落在弹簧上后继续向下运动到最低点的过程中,小球的速度v随时间t的变化图象如图乙所示,其中OA段为直线,AB段是与OA相切于A点的曲线,BCD是平滑的曲线.若以小球开始下落的位置为原点,沿竖直向下方向建立坐标轴Ox,则关于A、B、C、D各点对应的小球下落的位置坐标x及所对应的加速度a的大小,以下说法正确的是( )
A.xA=h,aA=0
B.xB=h+
,aB=0mg k
C.xC=h+2
,aC=gmg k
D.xD=h+2mg k,aD>g 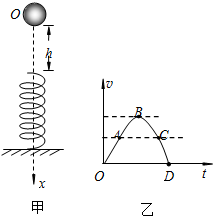
答案
A.OA过程是自由落体,A的坐标就是h,加速度为g,所以A错误.
B.B点是速度最大的地方,此时重力和弹力相等,合力为0,加速度也就为0,由mg=kx,可知x=
,所以B的坐标为h+mg k
,所以B正确.mg k
C.A、C两点关于B点对称,由A点到B点的形变量为
,由对称性得由B到D的形变量也为mg k
,所以在C点的形变量为mg k
,所以弹簧弹力F=2mg,F-mg=ma,a=g,x=2mg k
,所以C的坐标为h+2mg k
,所以C正确.2mg k
D.到达D点时,速度为0,所以到达D点时形变量要大于C点的形变量,所以D的坐标大于h+
,加速度aD>g,所以D错误.2mg k
故选BC.
