问题
填空题
在平面直角坐标系xOy中,函数f(x)=asinax+cosax(a>0)在一个最小正周期长的区间上的图象与函数g(x)=
|
答案
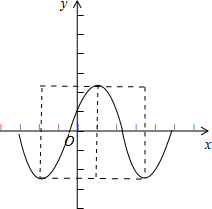
解法一:由三角函数公式可得f(x)=asinax+cosax=
sin(ax+ϕ),其中tanϕ=a2+1
,1 a
所以函数的周期为T=
,取长为2π a
,宽为22π a
的矩形,a2+1
由对称性知,面积的一半即为所求.
故答案为:2π a
.a2+1
解法二:由定积分的意义知,封闭图形的面积为∫ φ1φ2
[1-sin(ax+ϕ)]dxa2+1
换元,令ax+ϕ=t,则x=
(t-ϕ),上式可化为:1 a
a2+1 a
(1-sint)dt=∫
0π 2 2π a a2+1
故答案为:2π a
.a2+1
