问题
选择题
定积分
|
答案
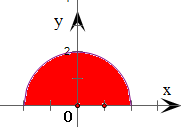
令y=
，得x2+y2=a2（y≥0）a2-x2
对应图形为以原点为圆心，半径为a的圆的上半圆
根据定积分的几何意义，∫ a-a
dx(a＞0)的值等于图中半圆的面积a2-x2
∴∫ a-a
dx=a2-x2
×π×a2=1 2
a2π 2
故选：D
搜题请搜索小程序“爱下问搜题”
定积分
|
令y=
，得x2+y2=a2（y≥0）a2-x2
对应图形为以原点为圆心，半径为a的圆的上半圆
根据定积分的几何意义，∫ a-a
dx(a＞0)的值等于图中半圆的面积a2-x2
∴∫ a-a
dx=a2-x2
×π×a2=1 2
a2π 2
故选：D