问题
填空题
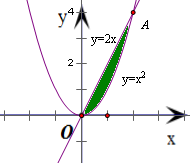
由曲线y=x2，y=2x围成的封闭图形的面积为______．
答案
由
，解得曲线y=x2及直线y=2x的交点为O（0，0）和A（2，2）y=x2 y=2x
因此，曲线y=x2及直线y=2x所围成的封闭图形的面积是
S=
（2x-x2）dx=（x2-∫ 20
x3） 1 3
=| 20
．4 3
故答案为：
．4 3
搜题请搜索小程序“爱下问搜题”
由曲线y=x2，y=2x围成的封闭图形的面积为______．
由
，解得曲线y=x2及直线y=2x的交点为O（0，0）和A（2，2）y=x2 y=2x
因此，曲线y=x2及直线y=2x所围成的封闭图形的面积是
S=
（2x-x2）dx=（x2-∫ 20
x3） 1 3
=| 20
．4 3
故答案为：
．4 3