问题
填空题
设A，B为三阶矩阵，A～B，λ1=-1，λ2=1为矩阵A的两个特征值，又
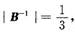则
答案
参考答案：
解析：[详解] 因为[*]所以|B|=3，又因为A～B，所以A，B有相同的特征值，设A的另一个特征值为λ3，由|A|=|B|=λ1λ2λ3，得λ3=-3，因为A-3E的特征值为-4，-2，-6，所以|A-3E|=-48．因为[*][*]
[*]
搜题请搜索小程序“爱下问搜题”
设A，B为三阶矩阵，A～B，λ1=-1，λ2=1为矩阵A的两个特征值，又
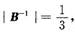则
参考答案：
解析：[详解] 因为[*]所以|B|=3，又因为A～B，所以A，B有相同的特征值，设A的另一个特征值为λ3，由|A|=|B|=λ1λ2λ3，得λ3=-3，因为A-3E的特征值为-4，-2，-6，所以|A-3E|=-48．因为[*][*]
[*]