参考答案：C

解析：

[分析]： 本题考查两个无穷小量阶的比较． 比较两个无穷小量阶的方法就是求其比的极限，从而确定正确的选项．本题即为计算：

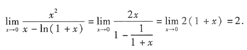由于其比的极限为常数2，所以选项C正确． 请考生注意：由于分母为x-ln(1+x)，所以本题不能用等价无穷小量代换ln(1+x)～x，否则各导致错误的结论． 与本题类似的另一类考题(可以为选择题也可为填空题)为：确定一个无穷小量的“阶”．例如： 当x→0时，x-ln(1+x)是x的

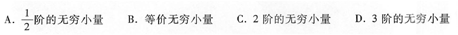这类题的解法是：首先设x-ln(1+x)为x的A阶无穷小量，再由

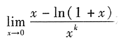存在且为一个有限值，从而确定k值． 因为 要使上式的极限存在，必须有k-2=0，即k=2． 所以，当x→0时，x-ln(1+x)为x的2阶无穷小量，选C．