问题
选择题
反证法证明“三角形中至少有一个角不小于60°”先应假设这个三角形中( )
A.有一个内角小于60°
B.每个内角都小于60°
C.有一个内角大于60°
D.每个内角都大于60°
答案
设三角形的三个角分别为:a,b,c.
假设,a<60°,b<60°,c<60°,
则a+b+c<60°+60°+60°,
即,a+b+c<180°与三角形内角和定理a+b+c=180°矛盾.
所以假设不成立,即三角形中至少有一个角不小于60°.
故选B.

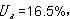 接有一台6500kW的6kV电动机,电动机起动前6kV已带负荷0.7(标幺值)。请计算电动机正常启动时6kV母线电压为下列哪项数值?(标幺值)
接有一台6500kW的6kV电动机,电动机起动前6kV已带负荷0.7(标幺值)。请计算电动机正常启动时6kV母线电压为下列哪项数值?(标幺值)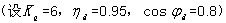 ()
()