问题
填空题
| 给出下列命题: ①若A,B是锐角△ABC的两内角,则有sinA>cosB; ②在同一坐标系中,函数y=sinx与y=lgx的交点个数为2个; ③如果
④存在实数x,使得等式sinx+cosx=
⑤若0<x≤1,则
其中正确的命题为______(写出所有正确命题的序号). |
答案
对于①:
A、B、C为锐角△ABC的三个内角,
∵A+B>
,∴A>π 2
-B,π 2
∴sinA>sin(
-B),π 2
即sinA>cosB.∴①正确;
对于②:
画出函数y=sinx和y=lgx的图象,
结合图象易知这两个函数的图象有3交点.
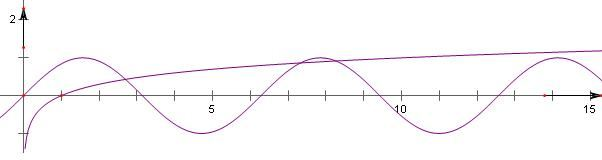
所以②错误;
对于③:
由题意可知:cosα≠0,分子分母同除以cosα,
=-5,tanα-2 3tanα+5
∴tanα=--
.23 16
∴③正确;
对于④:
sinx+cosx=
sin(x+2
)≤π 4
,2
∵
>3 2
,2
∴④错误:
对于⑤:
∵当x为锐角时,则有
sinx<x<tanx,
∴0<
<1,sinx x
∴
<sin2x x2
,sinx x
故⑤正确;
故答案为①③⑤
