搜题请搜索小程序“爱下问搜题”
问题 填空题
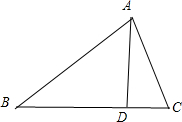
已知△ABC中，角A、B、C的对边分别为a、b、c，AH为BC边上的高，以下结论：
①
AC
•
AH
|
AH
|
=csinB；
②
BC
•(
AC
-
AB
)=b2+c2-2bccosA；
③
AH
•(
AB
+
BC
)=
AH
•
AB
；
④
AH
•
AC
=
AH
2．
其中正确的是______．（写出所有你认为正确的结论的序号）
答案

AC
•
AH
|
AH
|
=|
|
AC
||
AH
|cos＜
AC
，
AH
＞
|AH
|
=|
AC
|cos＜
AC
，
AH
＞=|
AH
|

而csinB=|

AH
|故①正确

BC
• (
AC
-
AB
)=
BC
2=a2

由余弦定理有a2=b2+c2-2bccosA

故有

BC
• (
AC
-
AB
)=  b2+c2-2bccosA故②正确

AH
•(
AB
+
BC
)=
AH
•
AC

∵

AH
•
AC
-
AH
 •
AB
=
AH
•(
AC
-
AB
)=
AH
•
BC
=0

∴

AH
•
AC
=
AH
•
AB
故③正确

AH
•
AC
=
AH
•(
AH
+
BH
)=
AH
2故④正确

故答案为：①②③④．

判断题

市场调查是督察考评的核心环节之一。
查看答案
多项选择题

每一位员工都要有整体经营思想和成本意识，成本构成的内容不仅指各项具体费用，还包括税收费用，你知道公司目前负担的有哪些税收项目（）

A、营业税

B、增值税

C、企业所得税

D、城市建设维护税及教育费附加
查看答案