问题
选择题
对于函数y=lg|x-3|和y=sin
(1)函数y=lg|x-3|的图象关于直线x=-3对称; (2)y=sin
(3)两函数的图象一共有10个交点; (4)两函数图象的所有交点的横坐标之和等于30; (5)两函数图象的所有交点的横坐标之和等于24.
|
答案
在同一坐标系中画出函数y=lg|x-3|和y=sin
(-4≤x≤10)的图象如下图所示:πx 2
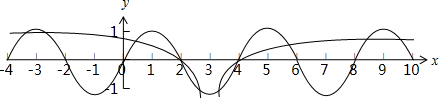
由图可知:
函数y=lg|x-3|的图象关于直线x=3对称,故(1)错误;
当x=3时,y=sin
取最小值-1,即直线x=3为函数y=sinπx 2
的一条对称轴,又由定义域关于x=3对称,故(2)正确;πx 2
两函数的图象一共有10个交点,故(3)正确;
且这些交点的平均数为3,故所有交点的横坐标之和等于30,故(4)正确,(5)错误
故正确的命题有:(2)(3)(4)
故选B