当1≤x≤

3

2

时，f（x）=4+8(x-

3

2

)=8x-8；当

3

2

＜x≤2时，f（x）=4-8(x-

3

2

)=-8x+16．

当2＜x≤3时，1＜

x

2

≤

3

2

，f（x）=

1

2

f(

x

2

)=

1

2

(8×

x

2

-8)=2x-4；

当3＜x≤4时，

3

2

＜

x

2

≤2，f（x）=

1

2

(-8×

x

2

+16)=-2x+8．

当4＜x≤6时，2＜

x

2

≤3，f（x）=

1

2

(2×

x

2

-4)=

1

2

x-2；

当6＜x≤8时，3＜

x

2

≤4，f（x）=

1

2

(-2×

x

2

+8)=-

1

2

x+4．…．

画出函数f（x）的图象：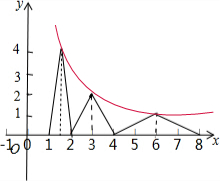

由图象可知：

①函数f（x）的值域为[0，4]，正确；

②关于x的方程f(x)=

1

2

有7个不相等的实根，因此②不正确；

③当x∈[1，2]时，函数f（x）的图象与x轴围成的图形的面积为S，则S=

1

2

×1×4=2，正确；

④画出函数y=

6

x

(x＞0)的图象，可知与函数y=f（x）有交点，

如x=

3

2

，3，6等，因此不存在x₀∈[1，8]，使得不等式f(x0)＞

6

x0

即x₀f（x₀）＞6成立，因此正确．

综上可知：①③④正确．

故答案为：①③④．