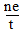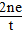A．∵sinxcosx=

1

2

sin2x≤

1

2

＜

3

5

，因此不存在x∈R，使得sinxcosx=

3

5

成立；

B．∵指数函数y=2^x在R上单调递增，若x∈（-∞，0），则2^x＜2⁰=1，因此不存在x∈（-∞，0），

使得2^x＞1成立，因此不正确；

C．∀x∈R，则x²-（x-1）=(x-

1

2

)2+

3

4

≥

3

4

＞0，因此C正确；

D．∀x∈（0，π），sinx＞cosx，不成立．例如x=

π

6

，sin

π

6

=

1

2

＜

3

2

=cos

π

6

．因此不正确．

综上可知：只有C正确．

故选：C．