如图5-1-8所示,光滑平行导轨仅其水平部分处于竖直向上的匀强磁场中,一根长为2 m的金属杆cd静止在水平轨道JK上,另一根质量为m的金属杆ab从斜轨高为h处由静止开始下滑,运动中两杆始终与轨道垂直且接触良好,两杆之间未发生碰撞.已知左边水平轨道的宽度是右边水平轨道宽度的两倍,在ab杆离开NQ前,两杆都做匀速运动,且磁场的磁感应强度大小为B.求两杆匀速时的速率.
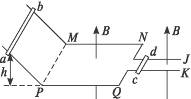
图5-1-8
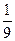
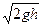
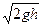
ab杆进入水平轨道之后,切割磁感线产生感应电动势,在回路中产生电流,cd杆在安培力作用下开始运动.在两者达匀速之前,ab杆做加速度减小的减速运动,而cd杆做加速度减小的加速运动,当两者都匀速时,设ab、cd杆的速率分别为v1、v2,则ab杆产生的感应电动势E1=BLabv1 ①
cd杆产生的感应电动势E2=BLcdv2 ②
由于都做匀速运动,则E1=E2 ③
取水平向右为正方向,在ab杆进入水平轨道到达匀速过程中,由动量定理得,
-B
Labt=mv1-mv ④
在cd杆由静止到刚开始匀速过程中,由动量定理得:BLcdt=2mv2 ⑤
在ab下滑高度h时,设其速度为v,有mgh=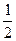
mv2 ⑥
且Lab=2Lcd ⑦
解以上各式得:v1=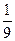
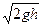
v2=.
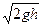