∵

x2-x4≥0 |x-2|-2≠0

∴函数定义域为

x|

-1≤x＜0或0＜x≤1，}

∴f(x)=

x2(1-x2)

-(x-2)-2

=

|x| 1-x2

-x

=

- 1-x2 0＜x≤1 1-x2 -1≤x＜0

作出函数图象，如图所示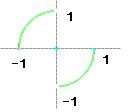

由图象可知函数定义域为[-1，0）∪（0，1]，值域为（-1，1）故（1）不正确；

∵函数定义域关于原点对称且

f(-x)=

|-x| 1-(-x)2

-(-x)

=

|x| 1-x2

x

=-f(x)

∴函数f（x）为奇函数，故（2）正确；

由图象可知函数在[-1，0）上为单调增函数，在（0，1]上也是单调增函数，但在定义域上不是增函数，如-1＜1，但f（-1）＞f（1）．故（3）不正确；

由图象可知函数的零点为x=-1，x=1，故（4）正确；

由图象可知图象为两个四分之一个圆弧构成，且半径为1，最大为AB连线过原点时最大为2，最小为

2

，但取不到．

故（5）正确．

故选C．