问题
选择题
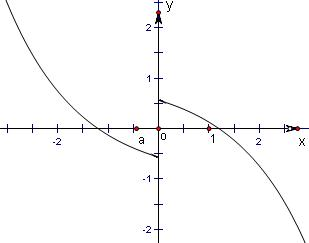
已知函数f(x)=a•2|x|+1(a≠0),定义函数F(x)=
①F(x)=|f(x)|; ②函数F(x)是奇函数; ③当a<0时,若mn<0,m+n>0,总有F(m)+F(n)<0成立, 其中所有正确命题的序号是( )
|
答案
由题意得,F(x)=
,a•2x+1,x>0 -a•2-x-1.x<0
而|f(x)|=
,它和F(x)并不是同一个函数,故①错误;a•2|x|+1,f(x)>0 -a•2|x|-1,f(x)<0
∵函数f(x)=a•2|x|+1是偶函数,
当x>0时,-x<0,则F(-x)=-f(-x)=-f(x)=-F(x);
当x<0时,-x>0,则F(-x)=f(-x)=f(x)=-F(x);
故函数F(x)是奇函数,②正确;
当a<0时,F(x)在(0,+∞)上是减函数,
若mn<0,m+n>0,总有m>-n>0,
∴F(m)<F(-n),即f(m)<-F(n),
∴F(m)+F(n)<0成立,故③正确.
故选C.