∵f（x）=x²-2x-3，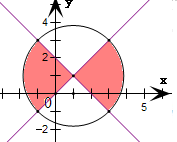

∴集合M={（x，y）|f（x）+f（y）≤0}

={（x，y）|x²+y²-2x-2y-6≤0}，

又∵方程x²+y²-2x-2y-6=0即（x-1）²+（y-1）²=8，

表示以（1，1）为圆心、半径为2

2

的圆．

∴集合M表示以（1，1）为圆心、半径为2

2

的圆及其内部．

又∵N={（x，y）|f（x）-f（y）≥0}={（x，y）|x²-y²-2（x-y）≥0}

={（x，y）|（x-y）（x+y-2）≥0}，

∴集合N对应的图形是直线x-y=0和直线x+y-2=0相交，位于左右两部分的平面区域．

因此，集合M∩N的区域是如图所示的阴影部分，它的面积是半径为2

2

的圆的面积的一半．

∴集合M∩N的面积S=

1

2

•π•(2

2

)2=4π．

故选：C