问题
选择题
数轴上坐标是整数的点称为整点,3条线段的长度之和是19.99,把这三条线段放在数轴上,覆盖的整点最多有( )个,最少有( )个.
A.23,19
B.23,12
C.22,7
D.22,6
答案
若线段长为整数m,则最多可覆盖m+1个整点(线段开始于整点时)
若线段长为s不为整数,则最多可覆盖[s]+1个整点([s]代表小于s的最大整数)
设3条线段长为x、y、z,共覆盖整点数为n
n≤x+1+y+1+z+1=x+y+z+3=19.9+3=22.9
又因为n为整数 n最大为22.
易知将线段长度定为1、1、17.9可得到22的结果,所以最多22个.
若将线段长度定为6.66、6.66、6.67,且将三条线段重叠,那么覆盖整点数≤6.9.所以最少7个.
故选:C.

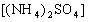 500元/吨,硝铵
500元/吨,硝铵 1000元/吨,某农民用500元钱去购买氮肥,为了使所购化肥得到的氮最多,他应选购哪种氮肥?
1000元/吨,某农民用500元钱去购买氮肥,为了使所购化肥得到的氮最多,他应选购哪种氮肥?