相距3750米的甲、乙两车站之间有一条笔直的公路,每隔2分钟有一辆摩托车由甲站出发以20米/秒的速度匀速开往乙站,每一辆摩托车在抵达乙站后都立即掉头以10米/秒的速度匀速开回甲站.这样往返的车辆共有48辆;若于第一辆摩托车开出的同时,有一辆汽车由甲站出发匀速开始乙站,速度为15米/秒,那么汽车抵达乙站前最后将与从甲站开出的第______辆摩托车迎面相遇,相遇处距乙站______米.
摩托车从甲地到乙地所需时间为t1=
=s v1
=187.5秒3750m 20m/s
设汽车速度为v=15m/s,摩托车从乙地开往甲地的速度 v2=10m/s,
设汽车抵达乙站前最后与甲站开出的第n辆摩托车相遇,相遇时汽车行驶的时间为t.
由题意知,每隔2分即△t=120秒有一辆摩托车由甲站开出,则相遇时,第n辆摩托车行驶的时间 为t-△t(n-1),第n辆摩托车从到乙站后和汽车相遇所经历的时间为t-△t(n-1)-t1
依据题意,摩托车在t-△t(n-l)-t1这段时间内行驶的距离与汽车在时间t内行驶的距离之和正好等于甲、乙两地之间的距离.即:
vt+v2[t-△t(n-1)-t1]=s,
化简得(v+v2)t=s+v2t1+v2△t(n-1),
(15m/s+10m/s)t=3750m+10m/s×187.5s+10m/s×120s(n-1),
整理得25m/s×t=4425m+1200m×n,
汽车从甲地到乙地所需时间:,
t0=
=s v
=250s,3750m 15m/s
故t<t0=250s,
n为正整数,
当n=1时,可得t=225s,
当n=2时,可得t=273s>t0=250s,
则根据上述分析,当n≥2时,都不合题意,只能取n=1,此时t=225s,
汽车行驶距离为s1=vt,
此时汽车离乙站距离:
s2=s-s1=s-vt=3750m-15m/s×225s=375m,
即汽车抵达乙站前最后将与从甲站开出的第1辆摩托车相遇,相遇处距乙站375m.
故答案为:1;375.

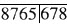 缺失,余留牙不松动,无龋坏,
缺失,余留牙不松动,无龋坏,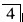 叩痛,局部义齿
叩痛,局部义齿 三臂卡环,游离端翘动。基牙疼痛的原因是()
三臂卡环,游离端翘动。基牙疼痛的原因是()