问题
选择题
两根足够长的光滑导轨竖直放置，间距为L,底端接阻值为R的电阻。将质量为m的金属棒悬挂在一个固定的轻弹簧下端，金属棒和导轨接触良好，导轨所在平面与磁感应强度为B的匀强磁场垂直，如图所示。除电阻R外其余电阻不计。现将金属棒从弹簧原长位置由静止释放，则
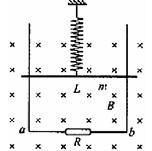
| A．释放瞬间金属棒的加速度等于重力加速度g | |
| B．金属棒向下运动时，流过电阻R的电流方向为a→b | C．金属棒的速度为v时，所受的按培力大小为F= |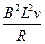
| D．电阻R上产生的总热量等于金属棒重力势能的减少 |
答案
AC
根据楞次定律（或右手定则）可以判断，电阻R中的电流方向由b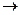
a，B项错误；金属棒速度为v时，导体棒中产生的电动势E=BLv，回路中电流I＝
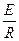，安培力F＝ILB＝
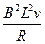，C项正确；在导体棒下落过程中受重力、弹簧弹力和安培力作用，但释放瞬间，弹簧弹力为0，安培力为0，只受重力作用，所以加速度等于重力加速度g，A项正确；根据能量守恒定律，金属棒重力势能的减少量一部分转化为动能，一部分转化为焦耳热能，D项错误．本题题目虽小，但全面考查了电磁感应的有关问题，体现了解决电磁感应问题的两条基本思路：对导体棒受力分析求解加速度或进行运动过程的动态分析；用能量转化和守恒的观点分析能量转化情况．
