如图甲所示,电阻不计、间隔距为l的平行长直金属导轨置于水平面内,阻值为R的导体棒ab固定连接在导轨左端,另一阻值也为R的导体棒ef垂直旋转在导轨上,ef与导轨接触良好并可在导轨上无摩擦移动。现有一根轻杆一端固定中ef中中断过程,另一端固定于墙上;轻杆与导轨保持平行,ef、ab两棒之间距离为d。若整个装置处于方向竖直向下的匀强磁场中,且从某一时刻开始,磁感应强度B随时间t按图乙所示的方式变化。
(1)求0 ~ t0时间内流过导体棒ef的电流大小和方向;
(2)求t0 ~ 2t0时间内导体棒ef产生的热量;
(3)分别写出0 ~ t0、t0 ~ 2t0时间内轻杆受力F随时间t 变化的函数关系式,求出2t0时刻轻杆受力F的大小和方向。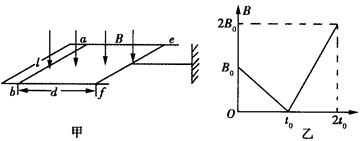
(1)I1 = 电流方向为e→ f
电流方向为e→ f
(2)Q =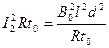
(3)F =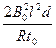 ,方向为向左的拉力
,方向为向左的拉力
(1)在0 ~ t0时间内,磁感应强度的变化率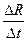 =
=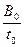
产生感应电动势的大小不E1 =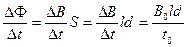
流过导体棒ef的电流大小I1 = (4分)
(4分)
由楞次定律可判断电流方向为e→f (1分)
(2)在t0 ~ 2t0时间内,磁感应强度的变化率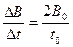
产生感应电动势的大小E2 =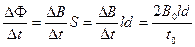
流过导体棒ef的电流大小I2 =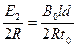 (4分)
(4分)
t0 ~ 2t0时间内导体棒ef产生的热量Q =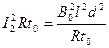 (2分)
(2分)
(3)在0 ~ t0时间内,磁感应强度B随时间t变化的函数关系为
轻杆受力F = B1I1l
0 ~ t0时间内轻杆受力F随时间t变化的函数关系式 F1 =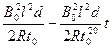
在t0 ~ 2t0时间内,磁感应强度B随时间t变化的函数关系为
B2 =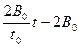 轻杆受力F = B2I2l
轻杆受力F = B2I2l
t0 ~ 2t0时间内轻杆受力F随时间t变化的函数关系式 F2 =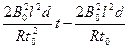
在2t0时刻轻杆受力F的大小为F =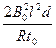 ,方向为向左的拉力(3分)
,方向为向左的拉力(3分)
