某电脑公司生产A种型号的笔记本电脑,2006年平均每台电脑生产成本为5000元,并以纯利润20%标定出厂价。从2007年开始,公司更新设备,加强管理,逐步推行股份制,从而使生产成本逐年降低,2010年平均每台A种型号的笔记本电脑尽管出厂价仅是2006年出厂价的80%,但却实现了纯利润50%的高效益.
(1)求2010年每台电脑的生产成本;
(2)以2006年的生产成本为基数,用二分法求2006~2010年生产成本平均每年降低的百分率(精确到0.01)。
解:(1)设2010年每台电脑的生产成本为P元,
根据题意,得P(1+50%)=5000×(1+20%)×80%,
解得P=3200(元),
故2010年每台电脑的生产成本为3200元.
(2)设2006~2010年生产成本平均每年降低的百分率为x,
根据题意,得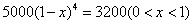 ,
,
令f(x)=5000(1-x)4-3200,
作出x,f(x)的对应值表:
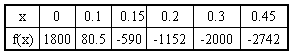
观察上表,可知f(0.1)·f(0.15)<0,说明此函数在区间(0.1,0.15)内有零点x0。
取区间(0.1,0.15)的中点x1=0.125,可得f(0.125)≈-269,
因为f(0.125)·f(0.1)<0,所以x0∈(0.1,0.125);
再取(0.1,0.125)的中点x2=0.1125,可得f(0.1125)≈-98,
因为f(0.1)·f(0.1125)<0,所以x0∈(0.1,0.1125);
同理可得,x0∈(0.1,0.10625),x0∈(0.103125,0.10625),x0∈(0.1046875,0.10625),
x0∈(0.10546875,0.10625),
由于|0.10546875-0.10625|<0.01,
此时区间的两个端点精确到0.01的近似值都是0.11,
所以原方程的近似解为0.11,
故2006~2010年生产成本平均每年降低的百分率为11%.
