问题
单项选择题
设向量组α1,α2,α3线性无关,且β1能被α1,α2,α3线性表出,而β2不能被α1,α2,α3线性表出.则( ).
A.α1,α2,β1线性相关
B.α1,α2,β2线性相关
C.α1,α2,β1,β2线性相关
D.α1,α2,α3,β1+β2线性无关
答案
参考答案:D
解析:
因α1,α2,α3线性无关,而β1能被α1,α2,α3线性表出.设β1=k1α1+k2α2+k3α3.对下面的矩阵施行初等列变换.
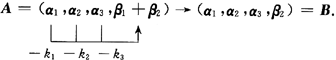
则有r(A)=r(B)(初等变换不改变矩阵的秩).
因已知α1,α2,α3线性无关,β2不能被α1,α2,α3线性表出,故α1,α2,α3,β2线性无关,即 r(B)=4,从而r(A)=r(α1,α2,α3,β1+β2)=4.即α1,α2,α3,β1+β2线性无关.
正确的选择应为D.
