问题
单项选择题
设在[a,b]上f(x)＜0，且在(a,b)内f′(x)＞0，f″(x)＜0，记I1=(b-a)f(b)，I2=
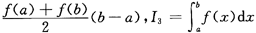，则( )．
A．I1＜I3＜I2
B．I1＜I2＜I3
C．I1＞I3＞I2
D．I3＜I1＜I2
答案
参考答案：C
解析：
由题设在(a,b)内f′(x)＞0,f″(x)＜0，可得在(a,b)内函数f(x)单调增加，曲线f(x)是凸的．如题21图所示曲线为f(x)图形．
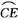
如题21图，记矩形ABCD的面积为S1，梯形ABCE的面积为S2，曲线
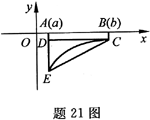，直线AE，直线BC及直线AB所围曲边梯形面积为S3，根据定积分的几何意义，I1=-S1，I2=-S2，I3=-S3，因S1＜S3＜S2，所以I1＞I3＞I2．故应选C．