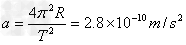问题
计算题
经天文学家观察,太阳在绕着银河系中心的圆形轨道上运动,这个轨道的半径约为3×104光年(约等于2.8×1020m),运动周期约2亿年(约等于6.3×1015s).太阳做圆周运动的向心力是来自位于其轨道内侧的大量星体的引力,可以把这些星体的全部质量看做是集中在银河系中心的来处理问题.(引力常量G为已知)
(1)从给出的数据来计算太阳轨道内侧这些星体的总质量;
(2)试求出太阳在其轨道上运动的加速度.
答案
解:(1)设太阳运动轨道内侧星体的总质量为M,
太阳质量为m,轨道半径为R,周期为T,太阳做圆周运动的,
由牛顿第二定律得: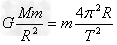
代入数据解得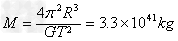
(2)太阳在圆周运动轨道上的加速度就是太阳的向心加速度,
所以