问题
解答题
已知z是实系数方程x2+2bx+c=0的虚根,记它在直角坐标平面上的对应点为Pz(Rez,Imz),
(1)若(b,c)在直线2x+y=0上,求证:Pz在圆C1:(x-1)2+y2=1上;
(2)给定圆C:(x-m)2+y2=r2(m、r∈R,r>0),则存在唯一的线段s满足:①若Pz在圆C上,则(b,c)在线段s上;②若(b,c)是线段s上一点(非端点),则Pz在圆C上。写出线段s的表达式,并说明理由;
(3)由(2)知线段s与圆C之间确定了一种对应关系,通过这种对应关系的研究,填写表(表中s1是(1)中圆C1的对应线段)。
答案
解:(1)由题意可得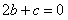 ,
,
解方程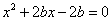 ,得
,得
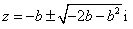
∴点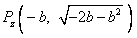 或
或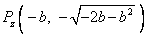
将点 代入圆
代入圆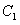 的方程,等号成立
的方程,等号成立
∴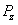 在圆
在圆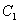
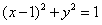 上;
上;
(2)当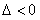 ,即
,即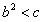 时
时
解得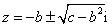
∴点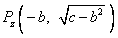 或
或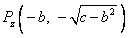
由题意可得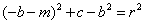
整理后得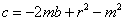
∵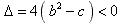 ,
,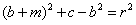
∴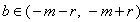
线段s为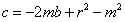 ,
,
若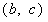 是线段s上一点(非端点),则实系数方程为
是线段s上一点(非端点),则实系数方程为
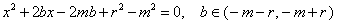
此时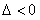 ,且点
,且点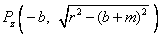 ,
, 在圆C上。
在圆C上。
(3)如表:
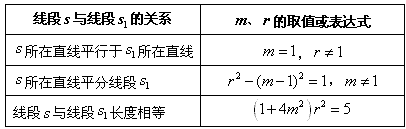 。
。
