问题
解答题
某商店经销一种世博纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上缴5元的税收,设每件产品的日售价为x元(35≤x≤41),根据市场调查,日销售量与ex(e为自然对数底数)成反比例,已知每件产品的日售价为40元时,日销售量为10件,
(Ⅰ)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(Ⅱ)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。
答案
解:(Ⅰ)设日销售量为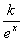 ,则
,则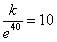 ,
,
∴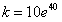 ,
,
则日销售量为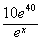 件,
件,
则日利润 (35≤x≤41);
(35≤x≤41);
(Ⅱ)L′(x)=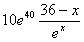 ,令L′(x)=0,得x=36,
,令L′(x)=0,得x=36,
当x∈[35,36),L′(x)>0,递增;当x∈(36,41],L′(x)<0,递减,
∴L(x)在x=36取最大,且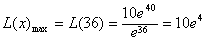 ,
,
答:当日售价为36元时,该商品日利润最大,最大为10e4元。
