问题
计算题
如图所示，一个被x轴与曲线方程y＝0.2sin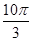 
x(m)所围的空间中存在着匀强磁场．磁场方向垂直纸面向里，磁感应强度B＝0.2 T．正方形金属线框的边长是L＝0.2 m，电阻是R＝0.1 Ω，它的一边与x轴重合，在拉力F的作用下，以v＝10 m/s的速度水平向右匀速运动．试求：
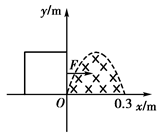
(1)拉力F的最大功率是多少？
(2)拉力F要做多少功才能把线框拉过磁场区？
(3)有位同学在老师的帮助下算出了曲线与x轴所围的面积为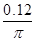
m2.请你再帮他算出线框右边框通过磁场区域的过程中通过线框某一截面的电荷量．(结果保留两位有效数字)
答案
(1)1.6 W (2)4.8×10－2 J (3)7.6×10－2 C
(1)当线框的一条竖直边运动到x＝0.15 m处时，线圈的感应电动势最大．
Em＝BLv＝0.2×0.2×10 V＝0.4 V
根据欧姆定律可得最大电流为Im＝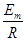
＝4 A
所以拉力F的最大值为Fm＝ImLB＝0.16 N
拉力F最大功率为Pm＝Fmv＝0.16×10 W＝1.6 W.
(2)把线框拉过磁场区域时，因为有效切割长度是按正弦规律变化的，所以，线框中的电流也是按正弦规律变化的(有一段时间线框中没有电流)．
电动势的有效值是E＝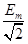
＝0.2
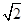V
通电时间为t＝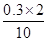
s＝0.06 s
拉力做功W＝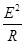
t＝0.048 J＝4.8×10－2 J.
(3)通过线框截面的电荷量
q＝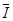
Δt，而＝
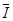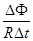，所以q＝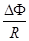
当磁场全部进入线框内部时，通过线框截面的电荷量最多，qm＝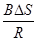
＝
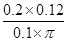C＝7.6×10－2 C.