解：（1）f（x）的定义域为（0，+∞），

f'（x）=lnx+1，令f'（x）=0，得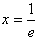

当x∈（0，+∞）时，f'（x），f（x）的变化情况如下：

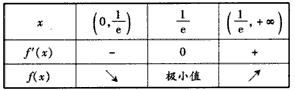
所以f（x）在（0，+∞）上的最小值是。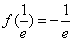

（2）当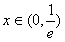时，f（x）单调递减且f（x）的取值范围是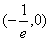

当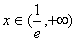时，f（x）单调递增且f（x）的取值范围是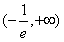

下面讨论f（x）-m=0的解：

所以，当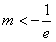时，原方程无解

当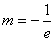或m≥0时，原方程有唯一解

当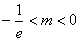时，原方程有两解。

（3）原不等式可化为：f（a）+f（a+b）-a]≥f（a+b）-（a+b）ln2，

设函数g（x）=f（x）+f（k-x）（k>0），

则g（x）=xlnx+（k-x）ln（k-x）（0＜x＜k）

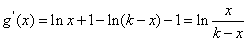
令g'（x）＜0，解得：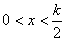

令g'（x）>0，则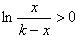

∴，

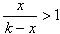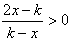
解得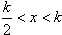

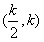∴函数g（x）在上单调递减，在上单调递增

∴g（x）在（0，k）上的最小值为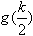

∴当x∈（0，k）时，总有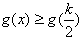

即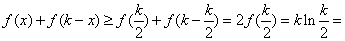

klnk-kln2=f（k）-kln2

令x=a，k-x=b，

则有：f（a）+f（b）≥f（a+b）-（a+ b）ln2。