问题
解答题
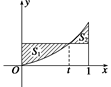
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积S1与S2之和最小.
答案
t=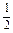 时,S最小,∴最小值为S(
时,S最小,∴最小值为S(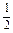 )=
)=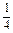
S1面积等于边长为t与t2的矩形面积去掉曲线y=x2与x轴、直线x=t所围成的面积,即
S1=t·t2-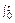 x2dx=
x2dx=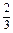 t3.
t3.
S2的面积等于曲线y=x2与x轴、x=t,x=1围成的面积减去矩形面积,
矩形边长分别为t2,(1-t),即
S2=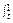 x2dx-t2(1-t)=
x2dx-t2(1-t)=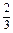 t3-t2+
t3-t2+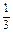 .
.
所以阴影部分的面积S为
S=S1+S2=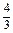 t3-t2+
t3-t2+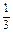 (0≤t≤1).
(0≤t≤1).
∵S′(t)=4t2-2t=4t(t-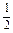 )=0时,得t=0,t=
)=0时,得t=0,t=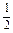 .
.
当t=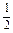 时,S最小,∴最小值为S(
时,S最小,∴最小值为S(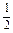 )=
)=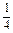 .
.