问题
解答题
求抛物线y2=x与直线x-2y-3=0所围成的平面图形的面积S.
答案
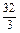
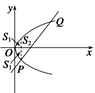
方法一 由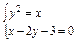 得抛物线与直线的交点为P(1,-1),Q(9,3)(如图).
得抛物线与直线的交点为P(1,-1),Q(9,3)(如图).
∴S=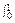 [
[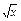 -(-
-(-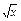 )]dx+
)]dx+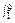 (
(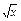 -
-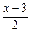 )dx
)dx
=2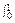
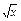 dx+
dx+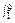 (
(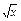 -
-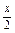 +
+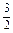 )dx
)dx
=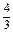
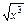 |
| +(
+(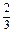 x
x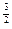 -
-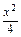 +
+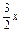 |
|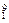 =
=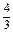 +
+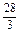 =
=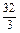 .
.
方法二 若选取积分变量为y,则两个函数分别为x=y2,x=2y+3.由方法一知上限为3,下限为-1.
∴S=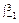 (2y+3-y2)dy=(y2+3y-
(2y+3-y2)dy=(y2+3y-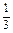 y3)|
y3)|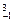
=(9+9-9)-(1-3+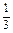 )=
)=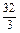 .
.
