求抛物线y2=2x与直线y=4-x围成的平面图形的面积.
18
由方程组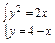 解出抛物线和直线的交点为(2,2)及(8,-4).
解出抛物线和直线的交点为(2,2)及(8,-4).
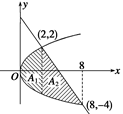
方法一 选x作为积分变量,由图可看出S=A1+A2
在A1部分:由于抛物线的上半支方程为y= ,
,
下半支方程为y=-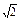 x,所以
x,所以
S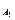 =
= [
[ -(-
-(- )]dx=2
)]dx=2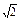
 x
x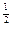 dx
dx
=2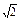 ·
· x
x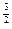 |
|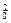 =
=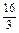 ,
,
S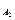 =
=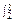 [4-x-(-
[4-x-(- )]dx
)]dx
=(4x-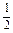 x2+
x2+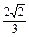 x
x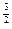 )|
)|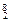 =
=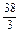 ,
,
于是:S=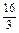 +
+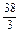 =18.
=18.
方法二 选y作积分变量,
将曲线方程写为x=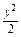 及x=4-y.
及x=4-y.
S=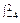 [(4-y)-
[(4-y)-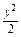 ]dy=(4y-
]dy=(4y-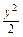 -
-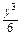 )|
)|
=30-12=18.
