问题
填空题
已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b,若b·c=0,则t= .
答案
2
由b·c=0知,
b·c=[ta+(1-t)b]·b=ta·b+(1-t)b2
=t×1×1×cos60°+(1-t)
=0.
即1-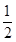
t=0,
∴t=2.
搜题请搜索小程序“爱下问搜题”
已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b,若b·c=0,则t= .
2
由b·c=0知,
b·c=[ta+(1-t)b]·b=ta·b+(1-t)b2
=t×1×1×cos60°+(1-t)
=0.
即1-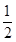t=0,
∴t=2.