问题
问答题
设α为3维列向量,αT是α的转置,若
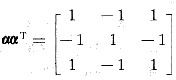 ,则αTα=______.
,则αTα=______.
答案
参考答案:[解] [*]
[*]
注意到[*]正好是矩阵ααT的主对角线元素之和.
所以本题αTα=1+1+1=3.
解析:[评注] 本题是考查矩阵的乘法运算,特别是考查符号ααT与αTα的区别.一般地,若α,β都是n维列向量,符号αβT与βαT都是秩为1的矩阵,而且(αβT)T=βαT,而符号αTβ与βTα都是数,且这两数相等αTβ=βTα,它是矩阵αβT的迹(也就是矩阵主对角元素之和),当然这也是矩阵βαT的迹.
在复习特征值之后,你能否立即回答下面的问题:
若α是3维列向量,αT是α的转置,如果αTα=3,那么矩阵ααT的3个特征值
