问题
解答题
常数a≥0,函数f(x)=x-ln2x+2alnx-1。
(1)令g(x)=xf'(x)(x>0),求g(x)的最小值并比较g(x)的最小值与0的大小;
(2)证明:当x>1时,恒有x>ln2x-2alnx+1。
答案
解:(1)∵f(x)=x-ln2x+2alnx-1(x>0),
∴f'(x)=1-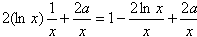
∴g(x)=xf'(x)=x-21nx+2a(x>0)
∴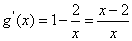
令g'(x)=0可得x=2
当x∈(0,2)时,g'(x)<0;
当x∈(2,+∞)时,g'(x)>0
∴g(x)在x=2处取得极小值g(2)=2-21n2+2a,
即g(x)的最小值为g(2)=2-21n2+2a,
g(2)=2(1-ln2)+2a
∵ln2<1,
∴1-ln2>0
又a≥0,
∴g(2)>0。
(2)由(1)可知,g(x)的最小值是正数,
所以对一切x>0恒有g(x)=xf'(x)>0
从而当x>0时,恒有f'(x)>0,故f(x)在(0,+∞)上是增函数,
∴当x>1时,f(x)>f(1)
又f(1)=1-ln21+2aln1-1=0,
∴f(x)>0,即x-1-ln2x+2alnx>0,
∴x>ln2x-2alnx+1
故当x>1时,恒有x>ln2x-2alnx+1。
