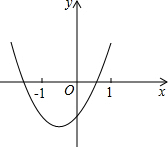问题
选择题
有下列4个命题中,真命题的序号是( )
①平面上有5个点(没有任何三个点在同一直线上),可以确定10条直线.
②若直角三角形的两条边长恰为方程x2-7x+12=0的两根,那么它的面积一定是6.
③点P(x,y)的坐标x,y满足x2+y2+2x-2y+2=0,则点P在正比例函数y=-x的图象上.
④若实数b、c满足1+b+c>0,1-b+c<0,则关于x的方程x2+bx+c=0一定有一个实数根x0满足-1<x0<1.
A.①②③④
B.①③④
C.①③
D.①④
答案
①平面上有5个点(没有任何三个点在同一直线上),可以确定
=10条直线,是真命题;5×(5-1) 2
②解方程x2-7x+12=0得x=2或x=5,因此直角三角形的面积为5或
,是假命题;21
③由x2+y2+2x-2y+2=(x+1)2+(y-1)2=0,解得:x=-1,y=-1,
故点P(x,y)在正比例函数y=-x的图象上是真命题;
④∵实数b、c满足1+b+c>0,1-b+c<0,
∴y=x2+bx+c的图象如图所示,
∴关于x的方程x2+bx+c=0有一实数根x0满足-1<x0<1,故为真命题.
故选B.