问题
选择题
已知向量a，b是夹角为60°的两个单位向量，向量a＋λb(λ∈R)与向量a－2b垂直，则实数λ的值为( )
A．1
B．－1
C．2
D．0
答案
答案：D
由题意可知a·b＝|a||b|cos 60°＝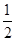
，而(a＋λb)⊥(a－2b)，故(a＋λb)·(a－2b)＝0，即a2＋λa·b－2a·b－2λb2＝0，从而可得1＋
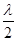－1－2λ＝0，即λ＝0.
搜题请搜索小程序“爱下问搜题”
已知向量a，b是夹角为60°的两个单位向量，向量a＋λb(λ∈R)与向量a－2b垂直，则实数λ的值为( )
A．1
B．－1
C．2
D．0
答案：D
由题意可知a·b＝|a||b|cos 60°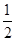＝，而(a＋λb)⊥(a－2b)，故(a＋λb)·(a－2b)＝0，即a2＋λa·b－2a·b－2λb2＝0，从而可得1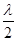＋－1－2λ＝0，即λ＝0.