问题
解答题
已知函数f(x)=(x+1)lnx-x+1。
(1)若xf'(x)≤x2+ax+1,求a的取值范围;
(2)证明:(x-1)f(x)≥0。
答案
解:(1)![]()
xf'(x)=xlnx+1,题设xf'(x)≤x2+ax+1等价于lnx-x≤a
令g(x)=lnx-x,则![]()
当0<x<1时,g'(x)>0;当x≥1时,g'(x)≤0,x=1是g(x)的最大值点,g(x)≤g(1)=-1
综上,a的取值范围是[-1,+∞);
(2)由(1)知,g(x)≤g(1)=-1,即lnx-x+1≤0
当0<x<1时,f(x)=(x+1)lnx-x+1= xlnx+(lnx-x+1)≤0;
当x≥1时,f(x)=lnx+(xlnx-x+1)
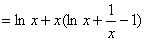
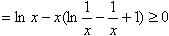
所以(x-1)f(x)≥0。
