问题
解答题
说出下列命题的逆命题,并判断逆命题的真假.若逆命题是真命题,请加以证明;若逆命题是假命题,请举出反例.
(1)如果a、b都是无理数,那么ab也是无理数;
(2)等腰三角形两腰上的高相等.
答案
(1)逆命题为:如果ab是无理数,那么a、b都是无理数.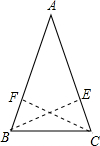
此逆命题为假命题.例如:如果ab=2
,那么a=2,b=3
.3
(2)逆命题是:如果一个三角形两边上的高相等,则这个三角形是等腰三角形.
此逆命题是真命题.证明如下:
已知:如图,在△ABC中,BE⊥AC于E,CF⊥AB于F,且BE=CF,
求证:AB=AC.
证明:∵S△ABC=
AB•CF=1 2
AC•BE,1 2
而BE=CF,
∴AB=AC,
∴△ABC是等腰三角形.
