问题
解答题
已知a≥0，函数f(x)=(x2-2ax)ex，
（Ⅰ）当x为何值时，f(x)取得最小值？证明你的结论；
（Ⅱ）设f(x)在[-1，1]上是单调函数，求a的取值范围。
答案
解：（Ⅰ）令f′(x)=0，即[x2-2(a-1)x-2a]ex=0，
∴x2-2(a-1)x-2a=0，
∵△=[2(a-1)]2+8a=4(a2+1)＞0，
∴x1=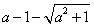
，x2=
，
又∵当x∈(-∞，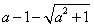
)时，f′(x)＞0；
当x∈(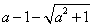
，
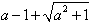)时，f′(x)＜0；
当x∈(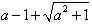
，+∞)时，f′(x)＞0，
列表：
∴x1，x2分别为f (x)的极大值与极小值点，
又∵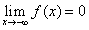
；当x→+∞时，f (x)→+∞，
而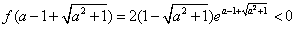
，
∴当x=
时，f (x)取得最小值。
（Ⅱ）f (x)在[-1，1]上单调，则f′(x)≥0(或≤0)在[-1，1]上恒成立，
而f′(x)=[x2-2(a-1)x-2a]ex，
令g(x)= x2-2(a-1)x-2a=[x-(a-1)]2-(a2+1)，
∴f′(x)≥0(或≤0)即g(x)≥0(或≤0)，
当g(x)≥0在[-1，1]上恒成立时，有
①当-1≤a-1≤1即0≤a≤2时，g(x)min=g(a-1)=-(a2+1)≥0(舍)；
②当a-1＞1即a≥2时，g(x)min=g(1)=3-4a≥0，∴a≤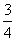
(舍)；
当g(x)≤0在[-1，1]上恒成立时，有
①当-1≤a-1≤0即0≤a≤1时，g(x)max=g(1)=3-4a ≤0，∴
≤a≤1；
②当0＜a-1≤1即1＜a≤2时，g(x)max=g(-1)=-1≤0，∴1＜a≤2；
③当1＜a-1即a＞2时，g(x)max=g(-1)=-1≤0，∴a＞2；
故a∈[
，+∞) 。