问题
解答题
求由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积.
答案
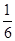
(1)化整为零,插入等分点.
将曲边梯形分成n个小曲边梯形,用分点
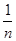 ,
,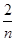 ,…,
,…, 把区间[0,1]等分成n个小区间
把区间[0,1]等分成n个小区间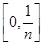 ,
, ,…,
,…,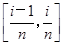 ,…,
,…,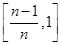 .简写作:
.简写作: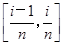 (i=1,2,…,n).
(i=1,2,…,n).
每个小区间的长度为Δx=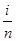 -
-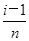 =
=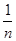 .
.
过各分点作x轴的垂线,把曲边梯形分成n个小曲边梯形,它们的面积分别记作:
ΔS1,ΔS2,…,ΔSi,…,ΔSn.
(2)以直代曲,估计误差.
用小矩形面积近似代替小曲边梯形面积.
在小区间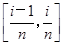 上任取一点xi(i=1,2,…,n),
上任取一点xi(i=1,2,…,n),
为了计算方便,取xi为小区间的左端点,用xi对应的函数值f(xi)= 为一边,以小区间长度Δx=
为一边,以小区间长度Δx=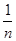 为邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为:ΔSi≈f(xi)·Δx=
为邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为:ΔSi≈f(xi)·Δx= ·
·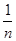 (i=1,2,…,n).
(i=1,2,…,n).
(3)积零成整,精益求精.
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和,就是曲边梯形面积S的近似值.即:
S=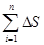 i≈
i≈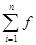 (xi)Δx=
(xi)Δx=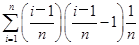 =-
=-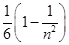 .①
.①
当分点数目越多,即Δx越小时,和式①的值就越接近曲边梯形的面积S.因此,当n趋于+∞时,即Δx趋于0时,和式①的极限值就是所求曲边梯形的面积.
Δx趋于0时,S趋于-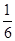 (负号表示图象在x轴下方).所以,由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形的面积是
(负号表示图象在x轴下方).所以,由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形的面积是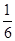 .
.
