已知函数f(x)=x+alnx,其中a为常数,且a≤-l,
(Ⅰ)当a=-l时,求f(x)在[e,e2](e=2.718 28…)上的值域;
(Ⅱ)若f(x)≤e-l对任意x∈[e,e2] 恒成立,求实数a的取值范围。
解:(Ⅰ)当a=-l时,f(x)=x-Inx,
得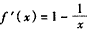 ,
,
令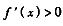 ,即
,即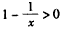 ,解得:x>1,
,解得:x>1,
所以函数f(x)在(1,+∞)上为增函数,
据此,函数f(x)在[e,e2]上为增函数,
而f(e)=e-1,f(e2)=e2-2,
所以,函数f(x)在[e,e2]上的值域为[e-1,e2-2];
(Ⅱ)由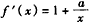 ,令
,令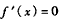 ,得
,得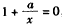 ,即x=-a,
,即x=-a,
当x∈(0,-a)时,f′(x)<0,函数f(x)在(0,-a)上单调递减;
当x∈(-a,十∞)时,f′(x)>0,函数f(x)在(-a,+∞)上单调递增;
若1≤-a≤e,即-e≤a≤-1,易得函数f(x)在[e,e2]上为增函数,
此时,f(x)max=f(e2),要使f(x)≤e-1对x∈[e,e2]恒成立,
只需 f(e2)≤e-1即可,
所以,有 ,即
,即 ;
;
而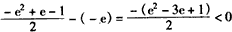 ,
,
即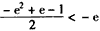 ,所以,此时无解;
,所以,此时无解;
若e<-a<e2,即-e>a>-e2,易知函数f(x)在[e,-a]上为减函数,在[-a,e2]上为增函数,
要使f(x)≤e-l对x∈[e,e2]恒成立,
只需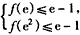 ,即
,即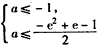 ,
,
由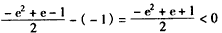 和
和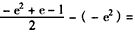
 ,
,
得 ;
;
若-a≥e2,即a≤-e2,易得函数f(x)在[e,e2]上为减函数,
此时,f(x)max=f(e),
要使f(x)≤e-1对x∈[e,e2] 恒成立,
只需 f(e)≤e-l即可,所以有e+a≤e-1,即a≤-1,
又因为a≤-e2,所以a≤-e2;
综合上述,实数a的取值范围是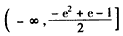 。
。
