问题
解答题
已知函数f(x)=x2-2elnx,求函数f(x)的单调区间和最值.
答案
解:由f(x)=x2-2elnx,得f′(x)=2x﹣ ,
,
令f'(x)=0,得x2=e,所以x=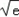 ,
,
当0<x<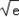 时,f'(x)<0,
时,f'(x)<0,
f(x)在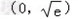 单调递减当x>
单调递减当x> 时,f'(x)>0,
时,f'(x)>0,
f(x)在 单调递增,
单调递增,
故函数f(x)=x2-2elnx在x= 时取得极小值,也是最小值
时取得极小值,也是最小值 ,无最大值
,无最大值
已知函数f(x)=x2-2elnx,求函数f(x)的单调区间和最值.
解:由f(x)=x2-2elnx,得f′(x)=2x﹣ ,
,
令f'(x)=0,得x2=e,所以x=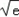 ,
,
当0<x<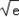 时,f'(x)<0,
时,f'(x)<0,
f(x)在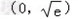 单调递减当x>
单调递减当x> 时,f'(x)>0,
时,f'(x)>0,
f(x)在 单调递增,
单调递增,
故函数f(x)=x2-2elnx在x= 时取得极小值,也是最小值
时取得极小值,也是最小值 ,无最大值
,无最大值