问题
解答题
已知三次函数f(x)=ax3+bx2+cx。
(1)若函数f(x)过点(-1,2)且在点(1,f(1))处的切线方程为y+2=0,求函数f(x)的解析式;
(2)在(1)的条件下,若对于区间[-3,2]上任意两个自变量的值x1,x2都有|f(x1)-f(x2)|≤t,求实数t的最小值;
(3)当-1≤x≤1时,|f′(x)|≤1,试求a的最大值,并求a取得最大值时f(x)的表达式。
答案
解:(1)∵函数f(x)过点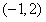
∴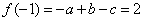 ①
①
又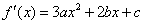 ,函数
,函数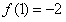 在点
在点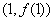 处的切线方程为
处的切线方程为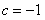
∴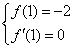
∴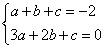 ②
②
由①和②解得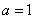 ,
,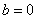 ,
,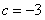
故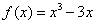 ;
;
(2)由(1)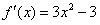 ,令
,令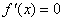
解得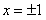
∴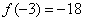 ,
,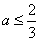 ,
,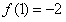 ,
,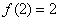
∴在区间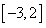 上
上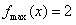 ,
,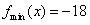
∴对于区间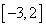 上任意两个自变量的值
上任意两个自变量的值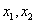
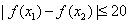
∴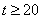
从而t的最小值为20;
(3)∵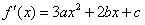
则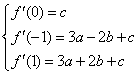
可得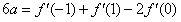
∵当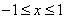 时,
时,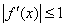
∴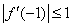 ,
,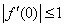 ,
,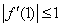
∴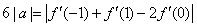
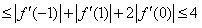
∴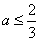 ,故a的最大值为
,故a的最大值为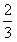
当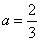 时,
时,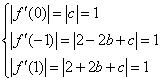 解得
解得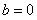 ,
,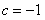
∴a取得最大值时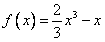 。
。
