问题
解答题
已知函数f(x)=x2-x+alnx
(1)当x≥1时，f（x）≤x2恒成立，求a的取值范围；
(2)讨论f（x）在定义域上的单调性；
答案
解：（1）由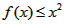
恒成立，得：
在
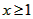时恒成立，
当x=1时a∈R
当x＞1时即a≤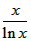
，令g（x）=，
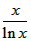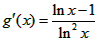
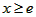时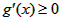
，g（x）在
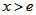时为增函数，g（x)在x＜e时为减函数
∴
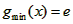，∴a≤e
（2）f(x)=x2-x+alnx，f′(x)=2x-1+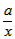
=
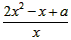，x＞0
当△=1-8a≤0，a≥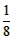
时，f′(x)≥0恒成立，f(x)在（0，+∞）上为增函数；
当a＜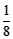
时
①当0＜a＜
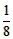时，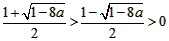
，f(x)在
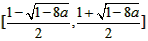上为减函数，
f(x)在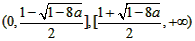
上为增函数
②当a=0时，f(x)在（0，1]上为减函数，f(x)在[1，+∞）上为增函数；
③当a＜0时，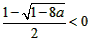
，故f(x)在（0，
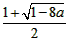]上为减函数，
f(x)在[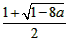
，+∞）上为增函数。