问题
解答题
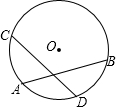
如图，已知：AB、CD是⊙O内非直径的两弦，求证：AB与CD不能互相平分．
答案
证明：设AB、CD交于点P，连接OP．
假设AB与CD能互相平分，则CP=DP，AP=BP．
∵AB、CD是⊙O内非直径的两弦，
∴OP⊥AB，OP⊥CD．
这与“过一点有且只有一条直线与已知直线垂直”相矛盾，所以假设不成立．
所以AB与CD不能互相平分．
搜题请搜索小程序“爱下问搜题”
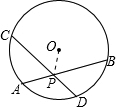
如图，已知：AB、CD是⊙O内非直径的两弦，求证：AB与CD不能互相平分．
证明：设AB、CD交于点P，连接OP．
假设AB与CD能互相平分，则CP=DP，AP=BP．
∵AB、CD是⊙O内非直径的两弦，
∴OP⊥AB，OP⊥CD．
这与“过一点有且只有一条直线与已知直线垂直”相矛盾，所以假设不成立．
所以AB与CD不能互相平分．