（12分）如图所示的传送带，其水平部分ab=2.09m，倾斜部分bc=3.2m，

问题计算题

（12分）如图所示的传送带，其水平部分ab=2.09m，倾斜部分bc=3.2m，与水平夹角为37°，皮带沿图示方向运动，速率恒为2m/s，把物体A轻放在点c处，它将被皮带送到a点，且物体A一直没脱离皮带。若物体A与传送带间的动摩擦因数μ=0.8，求物体A从c点被传送到a点所用的时间。. (g取10 m/s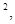sin37°="0.6," cos37°=0.8)

答案

5.05s

物体由c到b过程: ∑F=μmgcosθ-mgsinθ=ma a=0.4m/s²(2分)

V=at 2=0.4t t=5s X=(1/2)at²〉3.2m

3.2=(1/2)at₁² t₁=4s V=at₁=1.6m/s (4分)

物体由b到a过程: v=1.6+8t₂ t₂=0.05s(2分)

X₂=1.6t₂+4t²=0.09m (2分) t₃=2/v=1s

所以，全程时间t=t₁+t₂+t₃=5.05s(2分)

本题考查对牛顿第二定律的应用，在上划过程中，沿斜面方向的合力提供加速度，求得加速度后，再由运动学公式求解