问题
解答题
已知f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e]时,f(x)=ax+lnx。
(1)求f(x)的解析式;
(2)是否存在负实数a,使得当x∈[-e,0)时,函数f(x)的最小值为3?
答案
| 解:(1)设x∈[-e,0),则-x∈(0,e] |
| ∵f(x)是奇函数, |
| ∴f(x)=-f(-x)=-[a(-x)+ln(-x)] =ax-ln(-x) |
故 。 。 |
| (2)假设存在负实数a使得当x∈[-e,0)时,f(x)=ax-ln(-x)最小值是3, |
则由f'(x) ,知 ,知 |
①当 ,即 ,即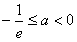 时,由x∈[-e,0)得f'(x)≥0, 时,由x∈[-e,0)得f'(x)≥0, |
| 此时函数f(x)=ax-ln(-x)递增, |
| 所以f(x)min=f(-e)=-ae- 1=3 |
解得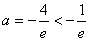 (舍去); (舍去); |
②当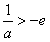 ,即 ,即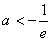 时, 时, |
则当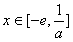 时,f'(x)≤0,函数f(x)=ax-ln(-x)递减;
时,f'(x)≤0,函数f(x)=ax-ln(-x)递减;
当 时,f'(x)>0,函数f(x)=ax-ln(-x)递增
时,f'(x)>0,函数f(x)=ax-ln(-x)递增
所以,函数当x∈[-e,0)时,
![]() ,解得a=-e2
,解得a=-e2
综上可知,存在实数a=-e2,使得当x∈[-e,0)时,函数f(x)有最小值是3。
